For more than a couple of years I’ve been dealing with a nightmare-like problem that I could not get solved with Excel.
The solution I was working with implies choosing between nearly infinite combinatorial possibilities. The problem in question has a lot of dependencies in a variable number of variables you can set, is an open problem in its definition, and I was looking for the optimal one. You bet I will never achieve it. I was also stuck wandering if I could face situations where several options were possible; and I couldn’t discard that as not pausible.
I considered GA as an alternative, but never put the enough time on studying the possibilities, considering I have not -or do not know, that is the same- a tool for GA in VBA. Times I spend a bit more learning GA in YouTube or in blogs did not scratch the surface, and the only XLS file I played with was very basic, and came from this old post from Paras Chopra blog, and another one from Dermont Balson’s InsaneExcel death blog (under Artificial Intelligence).
But none of them seemed enough to get in the thing… fortunately, I found two posts in spanish that put a lot more light into it (1 and 2).
 VBA implementation…
VBA implementation…
Genetic Algorithms is a technique that simulates the logic of Darwinian selection (in ‘The Origin of Species’, Darwin stated that from a group of individuals the best will survive) process. Kinda evolution.
Namely, a “simulated” population of chromosomes is randomly created and allowed to reproduce according to the laws of evolution with the hope that a very fit individual chromosome will eventually result. These chromosomes are actually (encrypted) candidate solutions to a problem, so when a good chromosome evolves, a good solution to a problem has evolved. It tries to emulate how populations accumulate differences over time due to the environmental conditions acting as a selective breeding mechanism. In other words, GA is a algorithm which makes it easy to search a large search space. By implementing the Darwinian selection to the problem, only the best solutions will remain, narrowing the search space as generations evolve. GAs can be used where optimization is needed, that is where there are large solutions to the problem but we have to find the best one(s). But they also have some disadvantages:- GAs are very slow. The efficiency of a gradient-based solver over a GA solver in some problems is notorious.
- They cannot always find the exact solution (but they iterate to the best solution).
- Chromosome: A set of genes. Chromosome contains the solution in form of genes.
- Gene: A part of chromosome. As the basic item of information, they contains a part of the solution.
- Individual/Genotype: Same as chromosome.
- Population: Nº of individuals present with “same length of chromosome”.
- Fitness: Fitness is the value assigned to an individual. It is based on how far or close a individual is from the solution. Greater the fitness value better the solution expressed.
- Fitness function: Fitness function is a function which assigns fitness value to the individual. It is problem specific.
- Breeding: Taking two fit individuals and intermingling their chromosome to create new individuals.
- Mutation: Changing a random gene in an individual.
- Selection: Selecting individuals for creating the next generation.
How Do GAs Work?
First a random population of chromosomes are created, and tested against the fitness of each one with a special fitness function. Although all the initial fitness values are probably very low (since the algorithm randomly created them), some are still higher than others. These chromosomes with higher fitness values are given a correspondingly higher probability to reproduce in the next generation. Thus for each generation in the evolution, a fitness function simulates natural selection by pushing the population in the direction of improved fitness (much like how natural selection nudges a biological species toward improved fitness with regards to its environment). As a general convention, reproduction in the GA is diploid (sexual), meaning that when two chromosomes are mated, pieces (genes) of each are combined in the offspring. Thus chromosomes recombine their parts at random (two point crossover) gene locations, occasionally producing a fitter chromosomes. This improvement to the gene pool is amplified by a corresponding increase in that fitter chromosome’s probability to reproduce. While there is no guarantee that genetic algorithms will find the optimal or “best” solution to a complex problem, they have been successfully applied to a wide variety of theoretical problems such as optimizing information networks because they iterate to better solutions. The trick, if one exists, is to write a fitness function that can successfully guide the evolutionary process.General Algorithm of GA
The algorithm is almost same in most applications, and only fitness functions are different to different problems. The general algorithm is as follows :START Generate initial population. Assign fitness function to all individuals. DO UNTIL best solution is found Select individuals from current generation Create new offsprings with mutation and/or breeding Compute new fitness for all individuals Kill all the unfit individuals to give space to new offsprings Check if best solution is found LOOP ENDHere comes very handy the code development made by Paras, that I post here with light modifications:
-
- Define an individualPublic Type Individual Genome() As Integer ‘Genome which holds information Fitness As Double ‘Fitness of Individual MadeBy As String ‘ Made By End TypeHere Genome is an array of integers. The algorithm uses integers instead of binary numbers. Integers are easy to handle and probably more efficient in GAs. It’s fitness contains the fitness value. And MadeBy holds the information about the process from which it is made.
- Define populationPublic Type Population NumOfIndivid As Integer ‘Number of individuals Individuals() As Individual ‘Individuals Parents() As Individual ‘Parents MaxFitness As Double ‘Maximum fitness NotifyWhenFitExceeds As Double ‘Notify the user if fitness exceeds this value GenomeLen As Integer ‘Length of Genome DiedIndivid() As Integer ‘Individuals who have died coz they had low fitness value NoOfDied As Integer ‘Present number of died individuals ProbMut As Double ‘Mutation probability per cent ProbCross As Double ‘CrossOver probability per cent StopEvolution As Boolean ‘ Check if we have to stop evolution Generation As Integer ‘ Generation number FitLim As Long ‘Fitness limit below which all will be killed BestSoFar As Individual ‘ Best Individual so far WorstSoFar As Individual ‘ Worst Individual so far End Type
- Build the population
-
- Evolve the population
Mutate all 33% of the population Kill all the worst individualsEND IF Kill all the worst individuals Select the parents Start breeding Mutate a random individual if probability allows. LOOP In the above algorithm the algorithm mutates 33% of population if less or all individuals are dying because in both the situations the necessary evolution does not take place. And crossing is done every time because without crossing new generation cannot be made.
-
- Selection of parents
-
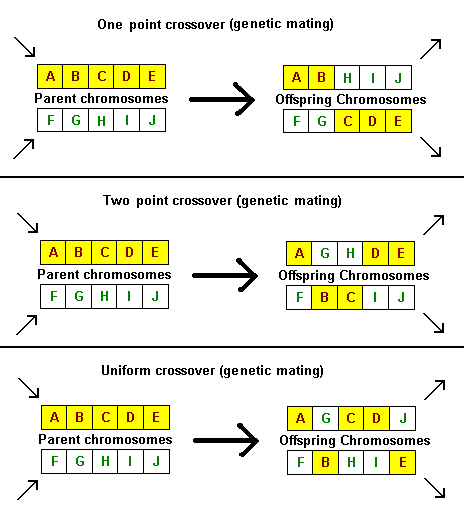
- CrossOver

-
- Mutation
 VBA implementation…
VBA implementation…
Private Type tGA_Settings
''Population parameters
NºChromosomesPopulation As Long '(mod 2 = 0)
CrossOverProbability As Double '(0.6-0.8)
CrossOverType As Long '(OnePoint/TwoPoints/Uniform/Random)
ChromosomesMutationProbability As Double '(0.01-0.02)
RandomSelectionProbability As Double '(0.1-0.2)
'Constraint parameters
ConstraintPenalty As Long '(Fixed/Linear/Exponential)
AbsoluteConstraintTolerance As Double
'Run parameters
MaxNumberGenerations As Long
ConvergenceTolerance As Double
NumericPrecision As Long
'Preliminary run (optional) parameters
NumberPreliminaryRuns As Long
MaxNumberGenerationsPerRun As Long
End Type
Private Type tGA_Variable
Min As Double
Max As Double
Evolution As Long 'eGA_Evolution: Fixed/Linear/Exponential
End Type
Private Type tGA_Constraint
Logical As Long 'eGA_Constraint: Less_Equal_Greater
Value As Double
End Type
Private Type tGA_Solver
FunctionOptimization As Long 'eFunctionOptimization: Minimize/Maximize
EvalFunction As String
Variable() As tGA_Variable
Constraint() As tGA_Constraint
Settings As tGA_Settings
End Type
Some more code to come as it gets done…
